Existence and Asymptotic Behavior of Positive Solutions for Variable Exponent Elliptic Systems
Cited by
Export citation
- BibTex
- RIS
- TXT
@Article{AAMM-8-19,
author = {Yin , Honghui and Yang , Zuodong},
title = {Existence and Asymptotic Behavior of Positive Solutions for Variable Exponent Elliptic Systems},
journal = {Advances in Applied Mathematics and Mechanics},
year = {2018},
volume = {8},
number = {1},
pages = {19--36},
abstract = {
In this paper, our main purpose is to establish the existence of positive solution
of the following system
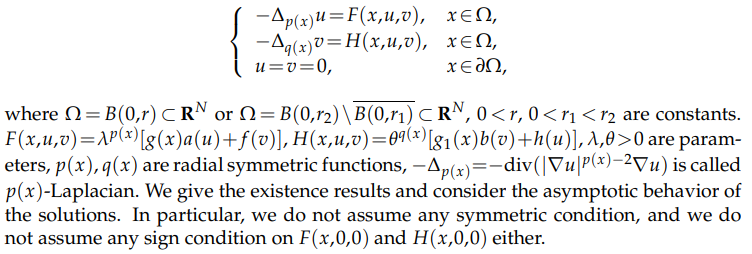
TY - JOUR
T1 - Existence and Asymptotic Behavior of Positive Solutions for Variable Exponent Elliptic Systems
AU - Yin , Honghui
AU - Yang , Zuodong
JO - Advances in Applied Mathematics and Mechanics
VL - 1
SP - 19
EP - 36
PY - 2018
DA - 2018/05
SN - 8
DO - http://doi.org/10.4208/aamm.2013.m322
UR - https://global-sci.org/intro/article_detail/aamm/12074.html
KW -
AB -
In this paper, our main purpose is to establish the existence of positive solution
of the following system
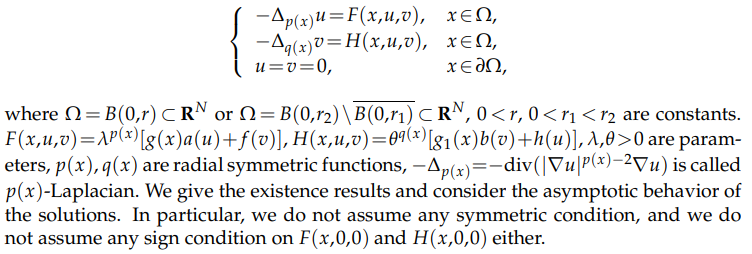
Honghui Yin & Zuodong Yang. (1970). Existence and Asymptotic Behavior of Positive Solutions for Variable Exponent Elliptic Systems.
Advances in Applied Mathematics and Mechanics. 8 (1).
19-36.
doi:10.4208/aamm.2013.m322
Copy to clipboard
