J. Nonl. Mod. Anal., 3 (2021), pp. 105-113.
Published online: 2021-04
[An open-access article; the PDF is free to any online user.]
Cited by
In this paper, we initiate the oscillation theory for $h$-fractional
difference equations of the form
where $_a∆^α_h$ is the Riemann-Liouville $h$-fractional difference of order $α$, $\mathbb{T}^a_h :$={$a + kh, k ∈ \mathbb{Z}^+ $∪{0}}, and $a ≥ 0$, $h > 0$. We study the oscillation of $h$-fractional difference equations with Riemann-Liouville derivative, and obtain
some sufficient conditions for oscillation of every solution. Finally, we give an
example to illustrate our main results.
- BibTex
- RIS
- TXT
In this paper, we initiate the oscillation theory for $h$-fractional
difference equations of the form
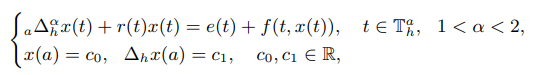
where $_a∆^α_h$ is the Riemann-Liouville $h$-fractional difference of order $α$, $\mathbb{T}^a_h :$={$a + kh, k ∈ \mathbb{Z}^+ $∪{0}}, and $a ≥ 0$, $h > 0$. We study the oscillation of $h$-fractional difference equations with Riemann-Liouville derivative, and obtain
some sufficient conditions for oscillation of every solution. Finally, we give an
example to illustrate our main results.
In this paper, we initiate the oscillation theory for $h$-fractional
difference equations of the form
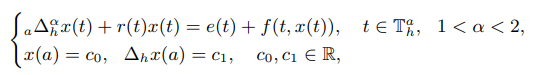
where $_a∆^α_h$ is the Riemann-Liouville $h$-fractional difference of order $α$, $\mathbb{T}^a_h :$={$a + kh, k ∈ \mathbb{Z}^+ $∪{0}}, and $a ≥ 0$, $h > 0$. We study the oscillation of $h$-fractional difference equations with Riemann-Liouville derivative, and obtain
some sufficient conditions for oscillation of every solution. Finally, we give an
example to illustrate our main results.