Anal. Theory Appl., 36 (2020), pp. 128-160.
Published online: 2020-06
[An open-access article; the PDF is free to any online user.]
Cited by
We consider minimizers of the energy
in a two-dimensional domain $\Omega$, with weak anchoring potential
This functional was previously derived as a thin-film limit of the Landau-de Gennes energy, assuming weak anchoring on the boundary favoring a nematic director lying along a cone of fixed aperture, centered at the normal vector to the boundary.
In the regime where $s [\alpha^2+(\pi-\alpha)^2]<\pi^2/2$, any limiting map $u_\ast:\Omega\to{\mathbb S}^1$ has only boundary vortices, where its phase jumps by either $2\alpha$ (light boojums) or $2(\pi-\alpha)$ (heavy boojums). Our main result is the fine-scale description of the light boojums.
- BibTex
- RIS
- TXT
We consider minimizers of the energy
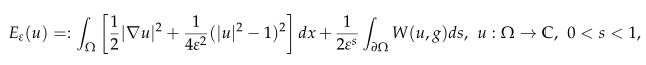
in a two-dimensional domain $\Omega$, with weak anchoring potential
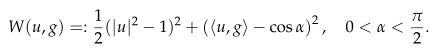
This functional was previously derived as a thin-film limit of the Landau-de Gennes energy, assuming weak anchoring on the boundary favoring a nematic director lying along a cone of fixed aperture, centered at the normal vector to the boundary.
In the regime where $s [\alpha^2+(\pi-\alpha)^2]<\pi^2/2$, any limiting map $u_\ast:\Omega\to{\mathbb S}^1$ has only boundary vortices, where its phase jumps by either $2\alpha$ (light boojums) or $2(\pi-\alpha)$ (heavy boojums). Our main result is the fine-scale description of the light boojums.
}, issn = {1573-8175}, doi = {https://doi.org/10.4208/ata.OA-0020}, url = {http://global-sci.org/intro/article_detail/ata/17127.html} }We consider minimizers of the energy
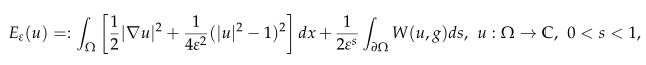
in a two-dimensional domain $\Omega$, with weak anchoring potential
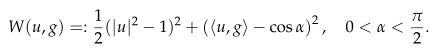
This functional was previously derived as a thin-film limit of the Landau-de Gennes energy, assuming weak anchoring on the boundary favoring a nematic director lying along a cone of fixed aperture, centered at the normal vector to the boundary.
In the regime where $s [\alpha^2+(\pi-\alpha)^2]<\pi^2/2$, any limiting map $u_\ast:\Omega\to{\mathbb S}^1$ has only boundary vortices, where its phase jumps by either $2\alpha$ (light boojums) or $2(\pi-\alpha)$ (heavy boojums). Our main result is the fine-scale description of the light boojums.