@Article{JCM-19-365,
author = {Li , Yao-Tang and Li , Ji-Cheng},
title = {On the Estimations of Bounds for Determinant of Hadamard Product of H-Matices},
journal = {Journal of Computational Mathematics},
year = {2001},
volume = {19},
number = {4},
pages = {365--370},
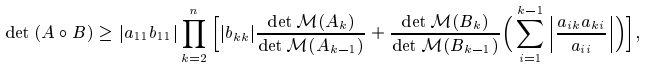
abstract = {<p style="text-align: justify;">In this paper, some estimations of bounds for determinant of Hadamard product of $H$-matrices are given. The main result is the following if $A = (a_{ij})$ and $B=(b_{ij})$ are nonsingular $H$-matrices of order $n$ and $∏^n_{i=1}a_{ii}b_{ii} ＞ 0,$ and $A_k$ and $B_k, k=1, 2, \cdots, n,$ are the $k \times k$ leading principal submatrices of $A$ and $B$, respectively, then&nbsp;<br/></p><p style="text-align:center"><img src="https://admin.global-sci.org/uploads/ueditor/image/20210722/1626947797540839.png" title="1626947797540839.png" alt="image.png" width="588" height="60"/></p><p style="text-align: justify;">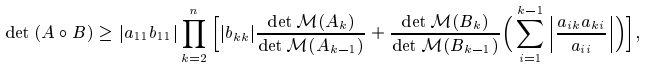where $M(A_k)$ denotes the comparison matrix of $A_k$.<br/></p>},
issn = {1991-7139},
doi = {https://doi.org/},
url = {http://global-sci.org/intro/article_detail/jcm/8989.html}
}