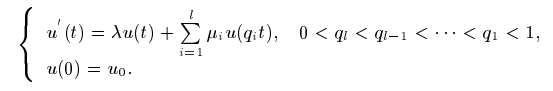
This paper deals with the asymptotic stability analysis of $\theta$ – methods for multi-pantograph delay differential equation
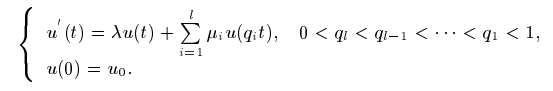
Here $\lambda, μ_1,μ_2, ... , μ_l, u_0 \in C$.
In recent years stability properties of numerical methods for this kind of equation has been studied by numerous authors. Many papers are concerned with meshes with fixed stepsize. In general the developed techniques give rise to non-ordinary recurrence relation. In this work, instead,we study constrained variable stpesize schemes, suggested by theoretical and computational reasons, which lead to a non-stationary difference equation. A general theorem is presented which can be used to obtain the characterization of the stability regions of $\theta$ – methods.