- Journal Home
- Volume 42 - 2024
- Volume 41 - 2023
- Volume 40 - 2022
- Volume 39 - 2021
- Volume 38 - 2020
- Volume 37 - 2019
- Volume 36 - 2018
- Volume 35 - 2017
- Volume 34 - 2016
- Volume 33 - 2015
- Volume 32 - 2014
- Volume 31 - 2013
- Volume 30 - 2012
- Volume 29 - 2011
- Volume 28 - 2010
- Volume 27 - 2009
- Volume 26 - 2008
- Volume 25 - 2007
- Volume 24 - 2006
- Volume 23 - 2005
- Volume 22 - 2004
- Volume 21 - 2003
- Volume 20 - 2002
- Volume 19 - 2001
- Volume 18 - 2000
- Volume 17 - 1999
- Volume 16 - 1998
- Volume 15 - 1997
- Volume 14 - 1996
- Volume 13 - 1995
- Volume 12 - 1994
- Volume 11 - 1993
- Volume 10 - 1992
- Volume 9 - 1991
- Volume 8 - 1990
- Volume 7 - 1989
- Volume 6 - 1988
- Volume 5 - 1987
- Volume 4 - 1986
- Volume 3 - 1985
- Volume 2 - 1984
- Volume 1 - 1983
Cited by
- BibTex
- RIS
- TXT
Fixed-point continuation (FPC) is an approach, based on operator-splitting and continuation, for solving minimization problems with $\ell_1$-regularization:
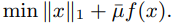
We investigate the application of this algorithm to compressed sensing signal recovery, in which $f(x) = \frac{1}{2}\|Ax-b\|_M^2$, $A \in \mathbb{R}^{m \times n}$ and $m \leq n$. In particular, we extend the original algorithm to obtain better practical results, derive appropriate choices for $M$ and $\bar{\mu}$ under a given measurement model, and present numerical results for a variety of compressed sensing problems. The numerical results show that the performance of our algorithm compares favorably with that of several recently proposed algorithms.
Fixed-point continuation (FPC) is an approach, based on operator-splitting and continuation, for solving minimization problems with $\ell_1$-regularization:
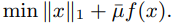
We investigate the application of this algorithm to compressed sensing signal recovery, in which $f(x) = \frac{1}{2}\|Ax-b\|_M^2$, $A \in \mathbb{R}^{m \times n}$ and $m \leq n$. In particular, we extend the original algorithm to obtain better practical results, derive appropriate choices for $M$ and $\bar{\mu}$ under a given measurement model, and present numerical results for a variety of compressed sensing problems. The numerical results show that the performance of our algorithm compares favorably with that of several recently proposed algorithms.
